Research

Markov Decision Processes and Reinforcement Learning

We study both theory and application of Markov decision processes. The theoretical pursuit has focused on the development of successive approximation algorithms and the dimension reduction of the functional space. In parallel, we also study machine learning techniques to tackle large scale dynamic optimization problem. In particular, we are tackling problems involving multiple decision makers using the reinforcement learning: multi-agent reinforcement learning.

Topics:

1. New successive approximation algorithms for the Markov decision processes
2. Sampling-based optimization for high-dimensional Markov decision processes
3. Dimension reduction for Markov decision processes
4. Reinforcement learning for multi-agent in collaborative and competitive environment
5. Deep reinforcement learning for large scale dynamic optimization

Applications

1. Dynamic Pricing of Multiple Product with Sales Milestones
2. Infrastructure management with multiple HVAC systems
3. Search and rescue optimization for a fleet of drones
4. Bayesian control chart for multi-variate process
5. Dynamic control of service systems
6. Predictive physical asset management

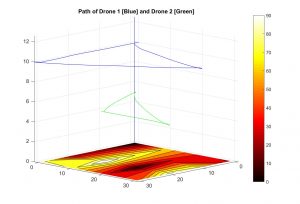	Optimal paths for two drones with search and rescue mission The drones are stationed in the upper corner where they can be charged. The drones are to be returned before the depletion of the battery to the station, while monitoring the area for search and rescue in a coordinated fashion.
Reinforcement learning for building management Three agents are controlling HVACs in a large retail store with an objective to minimize the total energy spending while maintaining a comfortable atmosphere in the building throughout the day.
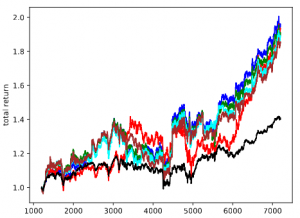
	Deep Recurrent Reinforcement learning for Algorithmic Trading A deep recurrent neural network-based reinforcement learning algorithm is capable of making continuous control over multiple assets with an objective of maximizing the portfolio return with some financial constraints.
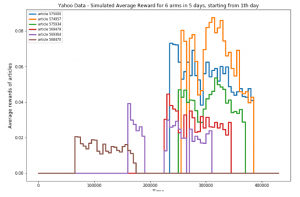
Non-stationary Multi-armed Bandit to Online Recommendation  Thompson sampling algorithm has been developed assuming piece-wise non-stationary bandits, and applied to a click-through rate maximization using data from Yahoo!

Financial Engineering

We study financial engineering problems that involve stochastic asset dynamics. We have studied the pricing of non-trivial derivatives such as swing options, callable convertible bonds, developed statistical arbitrage algorithms such as optimal pairs trading, and risk-rationing models.

Topics:

1. Analysis of first passage times
2. Lattice models for multiple non-stationary underlying assets
3. Finite difference method and its variants

Applications

1. Optimal thresholds for pairs trading
2. Valuation of real options with long maturity
3. Valuation of game options
4. Optimal risk rationing models for large investment companies
5. Valuation of options with optimally managed portfolio

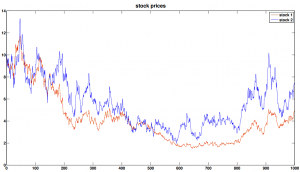	Optimal Pairs Trading To the left, price processes of two correlated assets (Coke and Pepsi) are shown. An OU process is defined from the two processes, and the expectation of the first passage time, which is expressed as an infinite sum of polynomial terms, leads to the calculation of optimal trading policy.
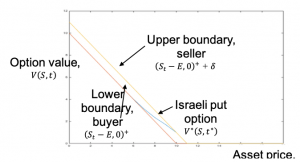
Robust Valuation of Israeli Options We study the robust equilibrium of Dynkim games for the valuation of Israeli options. The well posedness of reflected backward stochastic differential equation with two obstacles has been shown under a class of non-dominating probability measures.

 

Physical Asset Management

Physical asset management is often a large source of expense and plays a critical role in maximizing the productivity. We, via the Centre for Maintenance Optimization and Reliability Engineering, apply diverse combinations of statistical and machine learning approaches to predict upcoming failures, estimate the remaining useful life and optimize maintenance actions.

Topics:

1. Proportional hazard model
2. Predictive analytics using machine learning and statistical models
3. Optimization of the expected long-run cost

Applications

1. Data-driven digital twin
2. Signal analysis and prediction
3. Optimal MRO (Maintenance, Repair and Operations)

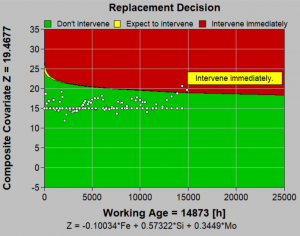Optimization of MRO Shown to the right is a screen shot of EXAKT, a standalone solution developed in the Centre for Maintenance Optimization and Reliability Engineering, to recommend optimal preventive maintenance measures considering remaining useful life and economic factors.